1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
| -module(guild_match).
-define(GROUP_NUM, 4). %% 组内盟数量 一个组4个盟
-define(DEBUG(F), io:format("##[~w~w:~w] "++F++"~n", [self(), ?MODULE, ?LINE])).
-define(DEBUG(F, A), io:format("##[~w~w:~w] "++F++"~n", [self(), ?MODULE, ?LINE|A])).
-compile(export_all).
%% @doc guild_match:gm_test_apply([a,4,b,4,c,3]) 表示A区报名了4个盟 B区报名了4个盟 C区报名了3个盟
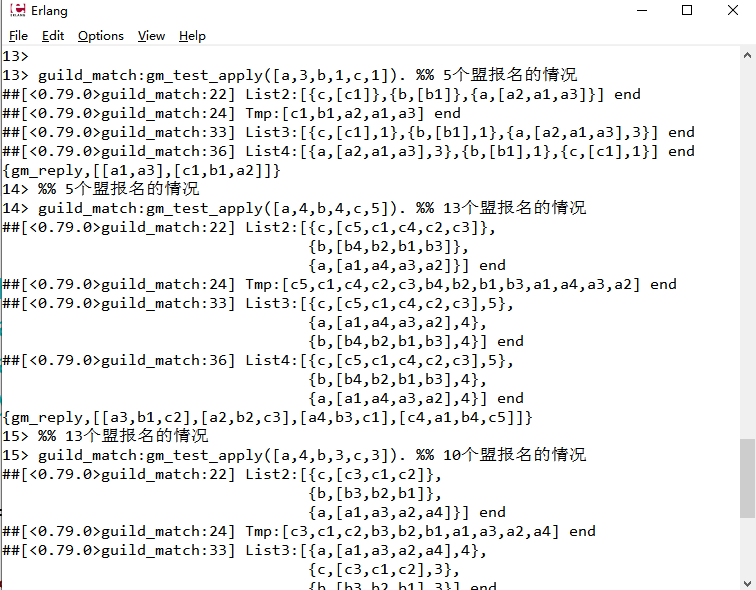
%% guild_match:gm_test_apply([a,3,b,1,c,1]). %% 5个盟报名的情况
%% guild_match:gm_test_apply([a,4,b,4,c,5]). %% 13个盟报名的情况
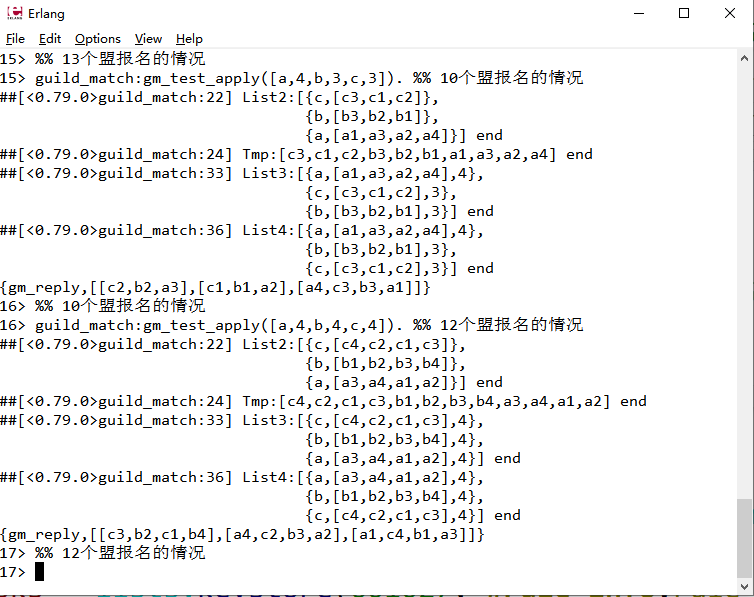
%% guild_match:gm_test_apply([a,4,b,3,c,3]). %% 10个盟报名的情况
%% guild_match:gm_test_apply([a,4,b,4,c,4]). %% 12个盟报名的情况
gm_test_apply(List) ->
List2 = gm_test_gen_apply(List, []),
?DEBUG("List2:~p end",[List2]),
Tmp = lists:flatten([X || {_, X} <- List2]),
?DEBUG("Tmp:~p end",[Tmp]),
%% 报名了多少盟
Length = length(Tmp),
{ok, Data} =
case Length >= 5 of
true ->
%% 一个组4个盟
Rem = Length rem ?GROUP_NUM,
List3 = [{H, Y, length(Y)} || {H, Y} <- shuffle(List2)],
?DEBUG("List3:~p end",[List3]),
%% 盟数量多的区在前面
List4 = lists:reverse(lists:keysort(3, List3)),
?DEBUG("List4:~p end",[List4]),
gm_test_apply_(List4, Rem, []);
false ->
{ok, [Tmp]}
end,
{gm_reply, Data}.
%% 构造一组 最大限度保证组内每个区都有一个盟
get_one([], One, _Mix) ->
{ok, One, []};
get_one(OldList, One, Mix) ->
%% 拿一个盟到NOne列表里面 如果NOne列表大于等于Mix(3或者4) 就返回
{ok, NOne, NewList} = get_one_(OldList, One, Mix, OldList),
case length(NOne) >= Mix of
true ->
{ok, NOne, NewList};
false ->
get_one(NewList, NOne, Mix)
end.
%% 按照4 4 4的格式排 如果余下9个盟或者余下6个盟 则转成 3盟1组的形式
get_mix(Flag, List) ->
Length = length(lists:flatten([X || {_, X, _} <- List])),
case Flag of
0 ->
4;
%% 余9 3 3 3
1 ->
case Length > 9 of
true ->
4;
false ->
3
end;
%% 余6 3 3
2 ->
case Length > 6 of
true ->
4;
false ->
3
end;
3 ->
case Length >= 4 of
true ->
4;
false ->
3
end
end.
gm_test_apply_([], _Flag, Result) ->
{ok, Result};
gm_test_apply_(List, Flag, Result) ->
Mix = get_mix(Flag, List),
{ok, One, Remain} = get_one(List, [], Mix),
gm_test_apply_(Remain, Flag, [One | Result]).
%% 区里的第一个盟拿到 NOne列表 中
get_one_([], Lou, _Mix, OldList) ->
{ok, Lou, OldList};
get_one_([{Area, [A1 | _HT1], _} | T], Lou, Mix, OldList) ->
case length(Lou) >= Mix of
true ->
{ok, Lou, OldList};
false ->
%% 删除拿出来的盟 这里面会打乱区内盟的顺序 因为每次都拿第一个 [A1 | _HT1] A1
NewList = del_use(OldList, Area, A1),
get_one_(T, [A1 | Lou], Mix, NewList)
end.
del_use(OldList, Area, A1) ->
case lists:keyfind(Area, 1, OldList) of
{_, List, _} ->
AList = lists:delete(A1, List),
case AList of
[] ->
lists:keydelete(Area, 1, OldList);
_ ->
One = {Area, shuffle(AList), length(AList)},
lists:keystore(Area, 1, OldList, One)
end;
false ->
OldList
end.
%%=======================================================================
%% @doc 打乱list的顺序
shuffle(L) when is_list(L) ->
List1 = [{rand:uniform(), X} || X <- L],
List2 = lists:keysort(1, List1),
[E || {_, E} <- List2];
shuffle(L) ->
?DEBUG("err Args:~w", [L]),
[].
%% 构造测试数据 输入 guild_match:gm_test_apply([a,4,b,4,c,4]).
%% 输出 [{c,[c4,c2,c3,c1]},{b,[b3,b1,b4,b2]}, {a,[a4,a2,a1,a3]}]
gm_test_gen_apply_(H1, 0, Result) ->
{H1, shuffle(Result)};
gm_test_gen_apply_(H1, H2, Result) ->
X = list_to_atom(lists:concat([H1, H2])),
gm_test_gen_apply_(H1, H2 - 1, [X | Result]).
gm_test_gen_apply([], Result) ->
Result;
gm_test_gen_apply([H1, H2 | T], Result) ->
One = gm_test_gen_apply_(H1, H2, []),
gm_test_gen_apply(T, [One | Result]).
|